Canvas Tag

目前正在研究如何在浏览器中画图：直线，椭圆等等。在Google上搜了一把，发现了一个canvas的标签。这个标签可以完成大多数画图的任务。不过很不幸，IE不支持这个标签。不知道在IE下画图有什么快速的好办法，如果谁知道，麻烦告诉我。

Now, I study how to draw graphics in browser. I search by Google, and find canvas tag. This tag can finish much draw task. But unfortunately, IE does not support this tag. I do not know there are some quickly methods to draw under IE. If someone know, tell me.

中美确实有必要建一条直连的光缆了

今天中国台湾省的一场地震震得中国大陆和美洲失去了联系。以中美两国的影响力，两国人民聊个天还得到日本绕个弯子实在说不过去，确实有必要建立中美直连的太平洋海底光缆了。

Problem 最小集合元素和

给定两个集合X,Y，每个都有n个元素。现在定义集合X+Y = {x+y | x in X and y in Y}现在问用什么方法可以最快的给X+Y排序。

这个问题还有一个描述就是，给定两个从小到大排好序的集合X,Y，每个都有n个元素。现在要找X+Y的最小的k个元素，问最快的方法是什么。

有人说后一个问题有O(klogk)复杂度的解决方案，正在探索中。O(n^2)的算法是显然的。

圣诞快乐

排序的交换问题

对一组序列排序的过程，就是通过对其中的元素两两交换实现的。这种交换次数被证明在最优的情况下是O(nlgn)，n是序列的长度。现在假设有一组排列{a1,a2,...,aN}，元素来自{1,2,...,N}。这组序列要实现从小到大的排序所需要的最小的交换次数记为K。现在问，给定N，K。满足这种性质的排列有多少个。

假设满足长度为N，最小交换次数为K的序列的数目为F(N,K)
我们可以得到如下的递归公式:
F(N,K) = (N-1)F(N-1,K-1) + F(n-1,K)

这样就可以用动态规划的算法求F(N,K)

An antiarithmetic permutation

给定一个正整数n，计算出一组{0,1,2,...,n}的排列，使得这个排列的任何子序列都不能形成等差数列，比如 n=4时，(2, 0, 1, 4, 3)符合要求，但是n=6时，(0, 5, 4, 3, 1, 2)不符合要求，因为（5,4,3)(5,3,1)都是等差数列。

这个题目可以有一个nlgn的算法，首先我们注意到{偶数，奇数，奇数}，{偶数，偶数，奇数}是不可能形成等差数列的，那么给定一个n，然后将序列分成2部分：
{偶数列} {奇数列}
可以看出任何子序列，如果既有元素属于偶数列，又有元素属于奇数列，是不可能构成等差数列的。下面我们只要保证偶数列和奇数列各自的子序列不会形成等差数列。这很容易，我们只需要将偶数列的每个数除以2，这是又形成了一个{0,1,2,[n/2]}的序列，可以用前面的方法把这个也分成奇数偶数列。同理，对奇数列只需要减1除以2，也可以用前面的方法排列，如此递归下去，就可以形成满足要求的排列。

高精度计算问题

在科学计算中常常需要进行高精度计算，这时计算机提供的int,double型精度不够，我们需要无限精度的数据结构来解决这个问题，为此，网上有很多相应的库。

1. CLN - Class Library for Numbers

2. NTL: A Library for doing Number Theory

3. GNU Multiple Precision Arithmetic Library

计算机程序设计艺术：学习

Knuth的这本著作一向被人放在书架上作为一种炫耀的资本，好像有了这本书，就能说明自己已经比较牛了。我一直也是这样，但决定从今天起，认真攻读它的第三卷：排序和查找。我相信，硬着头皮读下来，一定会对我有很大的帮助。

Donald Knuth(高德纳)

转自http://www.tianyablog.com/

Donald Knuth自传的开头这样写道：“Donald Knuth真的只是一个人么？”作为世界顶级计算机科学家之一，Knuth教授已经完成了编译程序、属性文法和运算法则的前沿研究，并编著完成了已在程序设计领域中具有权威标准和参考价值的书目的前三卷。在完成该项工作之余，Knuth还用了十年时间发明了两个数字排版系统，并编写了六本著作对其做了详尽的解释说明，现在,这两个系统已经被广泛地运用于全世界的数学刊物的排版中。随后，Knuth又发明了文件程序设计的两种语言，以及“文章性程式语言”相关的方法论。

到目前为止，Knuth已经出版发行了17部书籍，一百五十余篇论文，包括了巴比伦算法、圣经、字母“s”的历史等多方面的内容。作为一名数学家， Knuth曾开创了几门新的课程，为纯计算数学做出了很大贡献。他所获得的奖项和荣誉数不胜数，其中最值得注目的有1974年美国计算机协会图灵奖 (ACM Turing Award)，1979年美国前总统卡特授予的科学金奖(Medal of Science)以及1996年11月由于发明先进技术荣获的极受尊重的京都奖(Kyoto Prize)。在不多的业余时间里，Knuth不仅写小说，还是一个音乐家、作曲家、管风琴设计师。

是Knuth独特的审美感决定了他兴趣广泛、富有多方面造诣的特点，Knuth传奇般的生产力也是源于这一点。对于Knuth来说，衡量一个计算机程序是否完整的标准不仅仅在于它是否能够运行，他认为一个计算机程序应该是雅致的、甚至可以说是美的。计算机程序设计应该是一门艺术，一个算法应该像一段音乐，而一个好的程序应该如一部文学作品一般。

早期经历

Knuth，1938年1月10日生于美国威斯康星州密尔沃基市。他在模式方面辨别和熟练操作的能力在八年级的时候开始显现出来。当时，当地的一家糖果制造商举办了一项比赛，比赛要求选手用其品牌“Ziegler's Giant Bar”中的字母组成新的单词，规定时间内组成单词数量最多者获胜。Knuth参加了比赛，并以单词总数4500余个远远超过了裁判的2500个的标准，轻松赢得头奖。赛后，Knuth说道，如果自己当初想到回答时用些省略符号的话，还能写出更多。这次比赛Knuth为学校赢得了一台电视机，还为每个同学赢得了一根糖果棒。

Knuth多产的出版事业开始于他的高中时代，当时他的科技设计被Westinghouse Science Talent Search 光荣提及。他的“Potzebie System of Weights and Measures ”的基础章节被登在“Mad”杂志第26号，“Power”的基础章节被叫作“whatmeworry”。“Mad”的编辑认识到了年轻的Donald著作的重要性，以25美元买下了他的文章，并刊登在了其1957年6月的期刊上。

高中的时候，Knuth对数学并没多大兴趣，而是把主要精力放在主修的课程：听音乐和作曲上。他在高中的乐队里吹萨克斯、大号时，曾把 Dragnet、 Howdy Doody Time 和 Brylcream的主题曲联成一段新的音乐。这位著名的科学家在近期评论自己的早期作品时承认：“对于版权，我一无所知。”

虽然Knuth的等级平均分是学校历史上最高的，但是他和他的指导老师还是对他能否成功学习大学数学持怀疑态度。Knuth说在他高中阶段和大学早期一直有一种自卑感，这个问题一度是他的一个障碍。作为一个大学新生，Knuth没有对于失败的恐惧，他花了许多时间攻克额外的数学难题，几个月后，他在这方面的能力已经远远超过了其他同学。

高等教育和早期的计算机工作

当Knuth在Case科学院（现在的Case Western Reserve）获得物理奖学金时，梦想成为一个音乐家的计划改变了。Knuth回去继续研究数学是在大二，当时一个爱出难题的教授提出了一个特殊的问题，并说哪个学生能解决这个问题就立刻记成绩“A”。Knuth跟大多数同学一样，也认为那是道解不出来的题目，直到有一天，他错过了公共汽车，只能步行去看一个演出，Knuth利用路上这点空闲时间决定尝试一下。那阵子他运气真的是非常好，不仅问题很快就解开了，得到了“A”，还成功地经常逃课。虽然 Knuth也承认，逃课让他有负罪感，但是很明显，他完全有能力补上落下的功课，接下来的一学年，他的离散数学就又得了个“A”，而且还获得了给自己不能参加的课程评定论文等级的工作机会。

1956年，作为Case的新生，Knuth第一次接触到了计算机，那是一台IBM 650。Knuth说直到一年后，女孩才进入了他的生活。这又是计算机科学界一直以来亏欠科学家们的一个事例之一。

Knuth熬夜读IBM 650的说明手册，自学基本的程序设计。那时，在高等计算机语言发明之前，程序编写只能用第二代或是汇编语言。这个工作既耗时又困难，因为指令必须根据每台机器特定的构造编写，而实际上指令只须一步就可从二进制0、1系列转存到计算机硬盘上。Knuth说，有了第一次使用650的经历，他便肯定自己能编写出比说明手册上介绍的更好的程序。

Knuth很快便开始“闲逛”，编写可以执行数学函数的程序。他的第一个程序是把数字转化为素数，第三个是做井字游戏（或者说是让计算机在改正每次输的错误的过程来学会玩井字游戏）。作为学校篮球队的经理，Knuth编写了一个根据不同成绩标准评定每个运动员对球队贡献等级的程序，他的努力赢来了那些认为这样做有助于球队赢得同盟冠军的教练的好评（虽然，无庸质疑，不是每一个运动员都这样认为）。Knuth的成就成了新闻周刊的标志，他和教练、计算机的照片也被刊登在IBM650后来的说明手册上。

1960年，Knuth从Case毕业时享有着最高荣誉，在由全体教员参加的选举上，他因其公认的出众成就获得了硕士学位。1963年，Knuth 回到加利福尼亚理工学院攻取了数学博士学位，之后成为了该院的数学教授。在加利福尼亚理工学院任教期间，Knuth作为Burroughs 公司的顾问继续从事软件开发工作。1968年，他加入了斯坦福大学，九年后坐上了该校计算机科学学科的第一把交椅。1993年，Knuth成为斯坦福大学 “the Art of Computer Programming”（计算机程序设计艺术）的荣誉退休教授。

早期成就和计算机程序设计艺术的开端

1962年，Knuth还是个研究生的时候就开始了他计算机程序的工作。那时，他已经开始了个人咨询，为不同的机器编写编译程序。编译程序是一种翻译原始或高级语言和对象或二进制机器语言的中间语言。在不知道众多软件公司正高额寻求成百上千的编辑者的情况下，Knuth编写了一个程序，赚得5000 美元，他的名字立刻响誉了整个行业。世界上一流的出版社Addison-Wesley找到Knuth，请他写一本关于编译程序的书。到1966年， Knuth已经发表了3000页的手写设计草图，并且发明了一种综合方法，用于分析或决定结构翻译所客观需要的文法规则。最近，关于他的那第一部著作， Knuth自己这样评述：“用三年半的时间写第一章可并不是件好事。”

当Knuth的出版商计算出他的那3000页的笔迹打印成文章大约需要2000页时，大家才发现这实际上是一项多么大的工程。Knuth决定将它详述，成为一部更大的关于程序设计科学的纵览，共分为七个部分。一部巨著就这样——诞生了。《计算机程序设计艺术》，至今仍是各程序类图书书架上标志性的书籍。微软首席执行官比尔•盖茨在1995年接受一次采访时说，“如果你认为你是一名真正优秀的程序员，就去读第一卷，确定可以解决其中所有的问题。”值得注意的是，盖茨本人读这本书时用去了几个月的时间，并同时进行了难以置信的训练。盖茨还说：“如果你能读懂整套书的话，请给我发一份你的简历。”

依Knuth本人所讲，《计算机程序设计艺术》是他毕生最重要的事业，其目的是“组织和总结所知道的计算机方法的相关知识，并打下坚实的数学、历史基础”。Knuth撰写的前三卷被翻译成多种语言，到1976年为止，已卖出超过一百万册。他目前正全神贯注地编写第四卷，他期望第四卷的篇幅约为 2000页，并分为三个独立的章节。为了完成丛书的其余部分，Knuth现在进入了一种引退的状态，全身心地投入这项工作。Knuth说，一般说来，他更喜欢在一段时间内集中精神完成一项工作，正像他自己在书中提出的：按“一批”的模式。

Knuth从他主要的工作计划中拿出了十年，即从1976年起，致力于对数字排版的研究，设计了著名的文件准备TeX系统，字体生成程序METAFONT。这项工作带来的值得注意的副产品是用于结构文件和“文章性程式语言”附随方法论的WEB和CWEB语言。

现在，Knuth和他的妻子Jill，两个孩子John 和Jennifer一起，住在斯坦福大学校园里。他继续着《计算机程序设计艺术》第四卷的编写工作。虽然说Knuth是全身心的投入这一项工作，但他还是能挤出时间研究MMIX的设计，那是一台64位RISC（精简指令集计算机）。而他的业余爱好仍然是音乐，还一直邀请那些能够即兴演奏四手联弹钢琴曲的人们给他留下便条，以便安排一些活动。

成就简要回顾

编译程序
编译程序能够实现高级语言和二进制机器语言之间的翻译。二十世纪六十年代初期，Knuth教授致力于这方面的研究，虽然现代的软件已经可以使其变的简单一些，但编写编译程序仍被认为是一项极为困难的工作。Knuth教授在这方面最著名的成就是LR(k)分析的研究，那是一个能使确定一串字符文法规则的过程更加顺畅的值得注目的方法。

属性文法
在编译程序的工作之后，Knuth教授走上了形式上定义程序语言意义

Graph and Pagerank

Graph和Pagerank目前在检索里有了越来越广泛的应用。

首先，Graph已经成为特征表示的一个重要模型，现在很流行用Graph表示一篇文章，相对于传统的关键词集合，这种表示已经大大的包含了文本本来的信息。


而pagerank算法则是Grpah中排名的一个重要算法，比如，自动摘要中，想找出一个文章中最重要的一句话，那么可以把文章中所有的话看作一个个节点，从而构建一个图，然后用pagerank算法对每句话的重要性排名。

graph表示中的主要问题就是
1.如何定义顶点
2.如何定义边
3.如何定义边的权重

而pagerank的作用就是给每个顶点一个排名

看来pagerank，以及Page那句网络是个图的想法，对计算机网络的影响还是很深远

现在基本的思想就是
1.任何事物都可以用图表示
2.任何事物的排名都可以用pagerank算法

Google Set ：关键词 相似度

Google Set 是Google实验室中的一个产品，从他的意思，好像也是致力于词的语义关系的，谷歌给他的解释是： 基于词语例子，自动创建更多的同类词语集成。开来关键词的语义联系目前也是一个热门的研究方向。

How to Draw Graph（一）

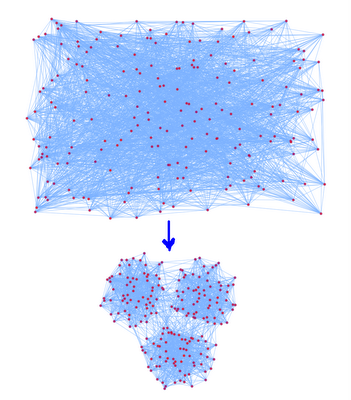
我们这里讨论的图是图论中的图，主要是研究如何将图显示在一个2D的平面上。首先举一个例子，考虑一个随机图：

我们定义3n个顶点，分成3个团(Group)，我们定义：

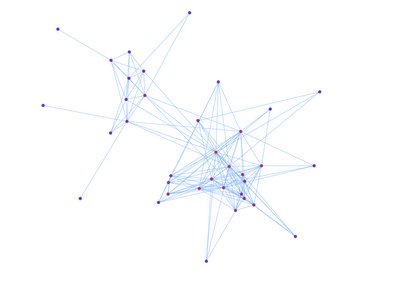
p(vi,vj)为vi和vj有边的概率，如果vi,vj属于同一个团，我们去比较大的概率，否则取比较小的概率。这样我们定义了一个有3个Group的随机图。

如果我们想把这个图在2D平面上显示出来，我们希望显示出来的图也能够显示出这种Group的结构。下面就是我们根据一定算法画出来的图：



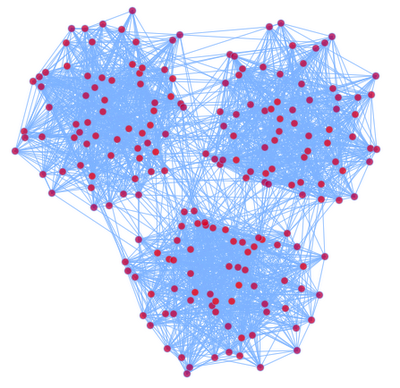
对于画图的问题，我们可以如下定义：

给定一个图G{V,E}，我们的任务是为每个顶点选择2D坐标vi(x,y)，以最小化一个我们定义的能量函数E(V,E)。

首先我们考虑最小化的算法，我们可以用经典的梯度下降法，算法如下：
1. 对顶点vi,i=1,2,......,|V|，随机生成每个顶点的坐标。
2. for t = 1 to T:
for i = 1 to |V|:
计算E相对于vi的梯度下降方向ei,并产生vi的下一个位置 vi(t+1) = vi(t) + alpha * e，alpha是步长

这就是梯度下降法的步骤，当然还可以用很多优化算法，比如共轭梯度法，或者进化计算的方法。下面我们主要考虑如何设计能量函数E，E的设计我们将得到分子结构的启发。

社会网络可视化软件

图的可视化也是目前一个研究方向。关于社会网络的可视化，有很多软件，比如KrackPlot,Pajek等等。但似乎对中文支持的都不好。为此，我还得把中文换成汉语拼音，太麻烦了。于是决定写一个自己的可视化工具。

可视化的核心就是一个Layout的问题，如何选择图顶点的坐标，让图看起来美观。我用了Qt做界面，算法用的梯度下降法。下面是我Layout出来的一些结果。感觉还行，嘿嘿。

六度分离(Six Degrees of Separation)理论

转自社会学吧

早在上个世纪60年代，美国著名社会心理学家米尔格伦(Stanley Milgram)就提出了“六级分隔”(Six Degrees of Separation)的理论，并设计了一个连锁信的实验来验证这个假设。他认为，任何两个陌生人都可以通过“朋友的朋友”建立联系，并且他们之间所间隔的人不会超过六个，无论是美国总统与威尼斯的船夫，或热带雨林中的土著与爱斯基摩人。也就是说，最多通过六个人你就能够认识任何一个陌生人。这就是著名的“小世界假设”。

从2001年秋天开始，美国哥伦比亚大学的社会学教授瓦茨(Duncan Watts)组建了一个研究小组，利用Email这一现代通信工具，开始进行“小世界假设”的实验(http://smallworld.columbia.edu)。在1年多时间里，总共有166个国家和地区的6万多名志愿者参与实验，实验结果证明，一封邮件平均被转发6次，即可回到接收者那里。

这个玄妙理论引来了数学家、物理学家和电脑科学家纷纷投入研究，结果发现，世界上许多其他的网络也有极相似的结构。经济活动中的商业联系网络、通过超文本链接的网络、生态系统中的食物链，甚至人类脑神经元，以及细胞内的分子交互作用网络，都有着完全相同的组织结构。