How to Draw Graph（一）

我们这里讨论的图是图论中的图，主要是研究如何将图显示在一个2D的平面上。首先举一个例子，考虑一个随机图：

我们定义3n个顶点，分成3个团(Group)，我们定义：

p(vi,vj)为vi和vj有边的概率，如果vi,vj属于同一个团，我们去比较大的概率，否则取比较小的概率。这样我们定义了一个有3个Group的随机图。

如果我们想把这个图在2D平面上显示出来，我们希望显示出来的图也能够显示出这种Group的结构。下面就是我们根据一定算法画出来的图：



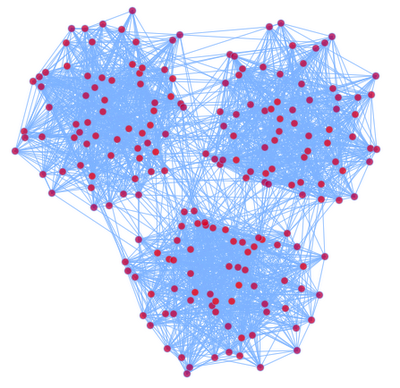
对于画图的问题，我们可以如下定义：

给定一个图G{V,E}，我们的任务是为每个顶点选择2D坐标vi(x,y)，以最小化一个我们定义的能量函数E(V,E)。

首先我们考虑最小化的算法，我们可以用经典的梯度下降法，算法如下：
1. 对顶点vi,i=1,2,......,|V|，随机生成每个顶点的坐标。
2. for t = 1 to T:
for i = 1 to |V|:
计算E相对于vi的梯度下降方向ei,并产生vi的下一个位置 vi(t+1) = vi(t) + alpha * e，alpha是步长

这就是梯度下降法的步骤，当然还可以用很多优化算法，比如共轭梯度法，或者进化计算的方法。下面我们主要考虑如何设计能量函数E，E的设计我们将得到分子结构的启发。